Control Systems 2

Describe how referenced negative feedback can become unstable

Negative feedback, which I discussed in my previous post for PHYL3004, does have its limitations. For example, phenomena under negative feedback control may oscillate around a set point rather than remaining stable at that point. There is also an issue with latency (delay before negative feedback kicks in) and range over which negative feedback can operate (for example, if you lose too much blood, no compensatory system can save you).

Define Power, Integral, Derivative, range, Input/output function and PID in reference to control systems

• Input/output function- I'm going to start with this one, and you'll appreciate why in a moment. The input/output function relates an input (for example, blood pressure) to an output (for example, number of impulses generated by the baroreceptors).
• Power- Power is the slope of the input/output function. In other words, how much does the output change after a change in input?
• Integral- The integral in this context is the integral of the error signal (i.e. deviation from the set point). This basically adds up the amount of error over time.
• Derivative- The derivative here is the derivative of the error signal. The rate of change of error can give an indication as to how much power is actually needed for stability. If the amount of error is falling, you don't need a lot of power- in fact, if you have too much power, you'll overshoot.
• Range- The range of values over which a feedback control system will operate.
• PID- Power, Integral, Derivative (though my engineer dad says that it's meant to be Proportion, Integral, Derivative). Basically, there are three main factors that determine output: power multiplied by the error signal, derivative of the error signal, and the integral of the error signal.

Give examples of input/output functions for a control system

I've already given an example above, which is blood pressure and firing rate of baroreceptors, but there are many others. Another such example is the partial pressure of carbon dioxide and pulmonary ventilation.

Explain how increasing power improves gain but reduces sensitivity

If you don't remember what gain is, it's basically the amount of change that is prevented by the feedback system. As power is the slope of the input/output curve, and smaller changes in input cause larger changes in output, an increase in power causes an increase in gain. If you keep increasing power, eventually you'll actually overshoot your set point. When power is increased too much, length overshoots so much that the system then needs to correct itself, but it may overcorrect due to the high power. This causes growing oscillations, which can be quite problematic. (I'm not sure how power affects sensitivity, because sensitivity was only mentioned in the "learning outcomes" slide. Maybe he's referring to the large oscillations that miss the mark every time? Or maybe he meant to say "stability," given that the slide says "More power more gain; more power less stable.")

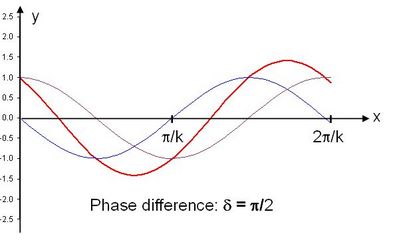
Oscillations can also be maintained by latency, or the delay before the response starts. For example, when a variable is at its peak, the system might prepare to respond to that peak value by attempting to decrease it, but by the time this response kicks in, the variable might not be at its peak any more. In other words, while the response was suitable at the time the input was received, it wasn't suitable any more by the time the system responded. If the latency and oscillations are out of phase, oscillations can become bigger. This can be especially bad if the oscillations are 90 degrees out of phase, probably because the constructive interference would look like this (image taken from http://astronomy.swin.edu.au/cosmos/C/Constructive+Interference):

Describe ways to limit instability in negative feedback control

There are a couple of main ways to limit instability in negative feedback control. PID control, mentioned in that list of definitions above, is one method. The derivative of the error signal can be used to predict the amount of error, which in turn can be used to control the amount of power, improving stability. The integral takes into account the amount of error over time. Therefore, all three factors in PID- power multiplied by error signal, integral of error signal, and derivative of error signal- can all add up to give a control system that is more stable than a system with only the first component alone.

Another way to limit instability is to use antagonistic pairs. There are many antagonistic pairs throughout the body: flexor and extensor muscles, parasympathetic and sympathetic nerves, insulin and glucagon, and so on. Each component of an antagonistic pair has its own oscillations, but they often cancel each other out.

Give an example of positive feedback control and how it is regulated
Explain how platelet activation occurs and is inhibited

Platelet activation is an example of positive feedback control. Platelets are activated by von Willebrand factor (vWF), which in turn is activated by binding to exposed collagen on a damaged vessel wall. As described here, activated platelets release ADP and thromboxane A₂ (TxA₂), which in turn stimulate activation of platelets and further release of ADP and TxA₂. Of course, there is a limit to this, otherwise our entire circulation would clot every time we got a little cut. ADP can also stimulate the release of nitric oxide (NO) and prostacyclin from healthy endothelium cells. As NO and prostacyclin inhibit platelet activation, the clot will remain restricted to the damage site.

Distinguish between feedback and feed-forward control

Feedback control: some kind of variable is measured, and that information is then used to control the same variable. Responds to past or present conditions, with a limited amount of anticipation.

Feedforward control: some kind of variable is measured, and that information is used to control something else. Responds to something that will probably happen in the future (anticipation).

Define feed-forward control and anticipation

I just did...

Give an example of a feed-forward control system in physiology

I'm going to be super-duper and give you three examples:

1. Respiration rate increases even before exercise begins.
2. Vestibular ocular reflex: semicircular canals allow us to keep track of our head movements, and this affects our eye muscles. Our eye movements coordinate to our head movements so that our visual field is kept stable.
3. Catching a ball uses both feed-forward and feedback. Feed-forward allows us to figure out where we need to put our hands (the "set point" in this system). Feedback lets us figure out where our hands are and how far they are from the "set point" determined by feed-forward.

Explain how delayed feedback control is used in learning motor skills

When we perform an action, such as throwing a ball, we can remember the outcome and use that to inform future actions. For example, if we throw a ball and it goes slightly left, we can try aiming differently the next time. Over time, we become more accurate.